Energy

Quadratic properties of solar energy

Analyze and describe the relationship between solar energy and time as a quadratic relation.

Grade

Duration

20 mins

Type

Thought starter

Overview

Using a graph that shows the amount of solar energy over the course of a year, students determine which of four equations (1 linear; 2 quadratics; and 1 cubic) best models the curve of best fit on the graph.

Instructions

What you'll need

"Properties of solar energy" worksheet
"Properties of solar energy graph" image
Digital projector and screen

Organize your students into pairs and provide each student with a copy of the "Properties of solar energy" worksheet.
Show the graph image, and guide students’ attention to the graph on their worksheet. Briefly explain that the various lines on the graph are curves of best fit that represent the data in a mathematical model. Tell students that research has shown that the quadratic model is the best fit to the solar energy data.
Ask your students:
1. “How can we determine which equation best describes the graph given in this information?”
2. “What might that equation look like?”
3. Draw your students’ attention to the equations to the right of the graph and invite groups to make an initial conjecture about which equation is the most useful for describing the graph.
Invite groups to share their initial decisions and thinking with the class. As they share, co-develop or present the criteria for a useful equation. A useful equation:
- Fits with all the relevant details from the graph; and
- Accurately shows the general pattern of the type of function modelled in the graph
- Prompt groups to rate each equation by considering the evidence shown in the graph and using the criteria for usefulness.
Students should identify the type of function represented by each equation and the direction of opening and vertex for the quadratic equations to match the details as closely as possible to the graph.
Encourage groups to share their decisions and thinking with the class.

Modify or extend this activity

Provide all equations as quadratic relations in vertex form with varying of correctness by changing the direction of opening and/or the vertex coordinates.

Curriculum Fit

Foundations of Mathematics 11

Big Idea

Optimization informs the decision-making process in situations involving extreme values

Content

Quadratic functions (characteristics including end behaviour, max/min; vertex; symmetry and intercepts)

Curricular competencies

Reasoning and modelling:

Explore, analyze, and apply mathematical ideas using reason, technology, and other tools

Understanding and solving:

Develop, demonstrate and apply mathematical understanding through inquiry and problem-solving

Communicating and representing

Use mathematical vocabulary and language to contribute to discussions in the classroom

Connecting and reflecting:

Reflect on mathematical thinking
Connect mathematical concepts with each other, other areas, and personal interests

Teaching Notes

This activity requires that students understand the essential properties of the graph of a quadratic relation, and terms including vertex, maximum/minimum direction of opening, axis of symmetry.
This activity requires that students understand the form of a quadratic relation in standard, vertex, and factored form.
The quadratic equation that models the relationship shown in the quadratic graph is:

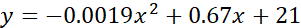
Solar power in B.C.

Solar energy is an affordable alternative energy that can be used to help heat and power your home, school, or business. However, there are some important considerations around the use of both solar photovoltaic and solar thermal systems in British Columbia that you should be aware of. Check out bchydro.com for more information regarding the practicality of solar energy in our province.

Assessment

Throughout the activity, consider how well students:

Understand the properties of the graph and equation of quadratic relation.
Use appropriate vocabulary (e.g., quadratic, vertex form, maximum, minimum, direction of opening) in their justifications and/or explanations.
Pay close attention to appropriate details
Use mathematical evidence to make sound mathematical decisions or conclusions.

Save Print